7. Indexamiento Multinivel y B-Trees
7.1 Indexado Multinivel
La idea de multiniveles es muy simple y no está necesariamente ligada con el concepto de árboles; puede aplicarse a los archivos ordenados de índices.
En qué se basa ?:
Hacer un índice del índice, índice del índice del índice, etc...
Quizás esto nos quede más claro con un ejemplo de la vida diaria:
- Si tenemos un conjunto de expedientes de clientes en una oficina le asignaremos a cada uno un folder
- Para organizarlos los metemos en un archivero y los ordenamos alfabéticamente, poniendo algun separador entre cada letra A, B, C, ...X, Y, Z. Estas letras forman un índice alfabético.
- Pero por lo general no nos caben todos los expedientes en un solo cajón del archivero, necesitamos repartirlos en varios, y para identificarlos colocamos etiquetas en cada cajón de acuerdo a los rangos de letras archivados ej A-F, G-M, etc...
Lo anterior se puede aplicar a los archivos ya ordenados de manera que los multiniveles nos permiten hacer búsquedas más rápidas.
Nota: de cierta manera los índices multiniveles forman una especie de árbol donde cada nivel es un índice del nivel inferior.
7.2 B-Trees, B*Trees, B+Trees
7.2.1 Antecedentes del problema
El problema de mantener un índice en almacenamiento secundario es demasiado lento. Esto se puede apreciar en 2 problemas específicos:
- Buscar el índice debe ser más rápido que una búsqueda binaria.
- Como se mencionó en secciones anteriores el número de accesos a disco es demasiado para una búsqueda binaria, si son demasiados entonces no tiene ningún beneficio este método. Necesitamos menos accesos a disco.
- Agregaciones y Eliminaciones deben ser tan rápidos como las búsquedas.
El problema de tener que mover los demas registros para colocar al registro nuevo en su lugar correspondiente "manteniendo el orden" no resulta nada práctico. Lo que se busca es una manera de realizar estas operaciones de modo que sólo tengan efectos locales y no reorganizaciones masivas.
7.2.2 Indexando con Arboles de Búsqueda Binaria
El mantener ordenada la lista de índices es muy problemático, quizás la primer solución que se nos viene a la mente es el hecho de crear el árbol binario en el disco.
Teniendo la lista de índices:
AX
|
CL
|
DE
|
FB
|
FT
|
HN
|
JD
|
KF
|
NR
|
PA
|
RF
|
SD
|
TK
|
WS
|
YJ
|
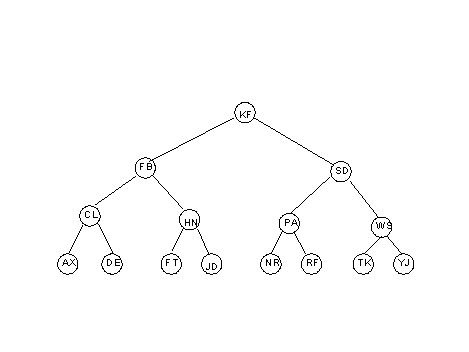
Su representación en un árbol binaria sería la siguiente:
Figura 7.1
En un archivo, al igual que hicimos con la pila o con la lista ligada también podemos tener una representación de esta estructura de datos, como se muestra a continuación:
|
Key
|
Left
|
Right
|
0
|
FB
|
10
|
8
|
1
|
JD
|
|
1
|
| 2 |
RF |
|
|
3
|
SD
|
6
|
13
|
4
|
AX
|
|
|
5
|
YJ
|
|
|
6
|
PA
|
11
|
2
|
7
|
FT
|
|
|
8
|
HN
|
7
|
1
|
9
|
KF
|
0
|
3
|
10
|
CL
|
4
|
12
|
11
|
NR
|
|
|
12
|
DE
|
|
|
13
|
WS
|
14
|
5
|
14
|
TK
|
|
|
Desafortunadamente este esquema sigue teniendo problemas:
- Se siguen realizando muchísimos acceso al disco para poder avanzar por las ramas del árbol
- El principal obstáculo sería que el árbol no quede balanceado (Figura 7.2), aquí la solución sería emplear árboles AVL y árboles binarios paginados.
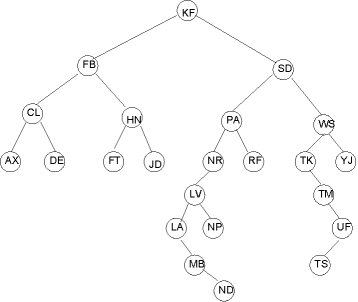
|
Figura 7.2
Para un árbol completamente balanceado el número de niveles que se deben explorar para encontrar una llave en el peor caso es:
Log2( N+ 1 ), (N = al número actual de llaves )
Y por otro lado para un árbol AVL el número de niveles es:
1.44 Log2 ( N + 2 )
De manera que se tiene una gran mejora al emplear árboles AVL, recordando que dichos árboles permiten tener un buen balanceo modificando un máximo de 5 apuntadores en los nodos.
La gran ventaja del método presentado es que el árbol se mantiene ordenado y el agregar una llave nueva sólo necesitamos ligarla a una de las hojas.
Recordando los problemas que hemos venido analizando:
- Número de accesos en la búsqueda binaria
- Mantener ordenado el archivo de índices
Tenemos una solución aceptable para el segundo problema, pero el primero aún no lo hemos superado, así que analicemos una técnica que nos permite disminuir ese número de accesos.
7.2.3 Arboles Binarios Paginados (Paged Binary Trees)
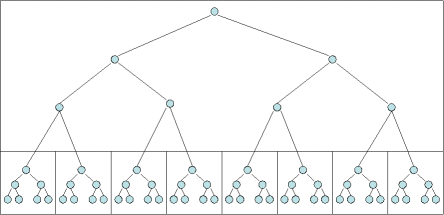
A continuación (Figura 7.3) se presenta un ejemplo con páginas de 7 nodos (3 niveles)
Figura 7.3
- En este ejemplo podemos localizar cualquiera de los 63 nodos con no más de 2 accesos a disco.
- Si hacemos la página de un nivel más grande (abajo), tendríamos 64 páginas más de 7 nodos cada una y podríamos encontrar cualquiera de los 511 nodos totales [(64+9)*7] con sólo 3 accesos al disco.
- Si volvemos a crecer tendríamos en 1 nivel 512 páginas más, y la posibilidad de encontrar alguno de 4095 [(512+64+9)*7] nodos con sólo 4 accesos al disco lo cual es un gran ahorro comparado con 12 accesos que tendríamos con un búsqueda binaria tradicional.
Si tomamos páginas de 511 llaves/referencias tendríamos la posibilidad de encontrar un nodo de entre 134,217,727 con tan solo 3 accesos a disco.
De manera que el número de accesos se puede calcular como:
Logk+1 (N+1) , donde N = número de llaves y k el número de llaves por página
Log 511+1 (134,217,727 + 1) = 3 accesos
Mientras que en el esquema tradicional (Log2(N+1)) tendríamos:
Log2(134,217,727 +1) = 27 accesos
Aparentemente habríamos resuelto todos nuestros problemas, podríamos mantener el índice ordenado fácilmente y para todas las operaciones el número de accesos es reducido.
Pero desafortunadamente esto no es así, aún tenemos algunos problemas o limitantes:
- Algunas operaciones siguen siendo costosas
- Si las llaves entran de manera aleatoria las páginas del árbol no quedarán balanceadas (Figura 7.4) y probablemente recuperemos páginas vacías o con muy pocos elementos.
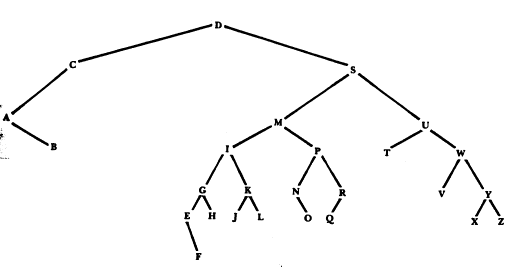
|
Figura 7.4 (cada letra representa una página)
7.2.4 B-Trees
El concepto de B-Tree surge en 1972 (después del viaje a la luna) y fue creado por Bayer y McCreight en los Laboratorios de Investigación Boeing.
Los autores nunca han mencionado el significado de la "B", algunas personas dicen que es por "balanced", "broad" o inclusive por "Bayer" o "Boeing".
Evidentemente se trata de un árbol o mejor dicho de la generalización de un árbol que permite varias "salidas" o ligas desde sus nodos, de hecho cada nodo contiene varios registros (llaves).
La Figura 7.5 muestra un árbol binario señalando la ruta que se seguiría para insertar un nodo nuevo con valor de "15".
|
Figura 7.5
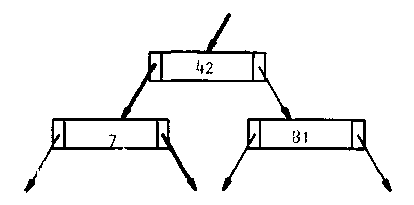
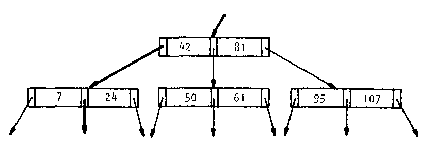
Este árbol es muy similar a los que ya hemos presentado anteriormente y que seguramente también es el más popular cuando hablamos de estructuras de datos. Pero este árbol no necesariamente tiene que tener únicamente un registro (para nuestro caso una llave), la Figura 7.6 muestra un árbol donde cada nodo posee dos llaves y 3 ligas o salidas hacia los siguientes niveles. Se puede observar que para el caso de la raíz el camino de la izquierda representará la ruta hacia aquellas llaves menores que 42, mientras que el de la derecha representará aquellas que sean mayores que 81 y la del centro aquellas que sean mayores a 42 pero menores a 81.
|
Figura 7.6
De manera general podemos decir que cada nodo de un B-Tree de orden "d" contiene a lo más 2d llaves y 2d+1 apuntadores o ligas. Es importante resaltar que cada nodo debe tener al menos "d" llaves en todo momento, exceptuando la raíz cuya única restricción que tenga la menos 1 llave (2 ligas).
Para los ejemplos de inserción y eliminación estaremos utilizando un b-tree de orden 2.
Figura 7.7
Balanceo
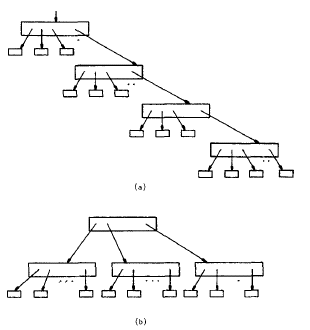
Una de las grandes ventajas de los B-Trees son sus métodos de inserción y eliminación ya que mantienen balanceado el árbol a diferencia de los tradicionales donde se podría tener un caso donde se tenga un acceso secuencial (Figura 7.8a) donde no se aprovecha en nada la estructura de árbol, mientras que el B-Tree siempre mantiene una forma piramidal (Figura 7.8b) gracias a su balanceo.
|
Figura 7.8
Gracias a dicho balanceo el "camino" más largo en un B-Tree de "n" llaves contiene a lo más logd n nodos, donde d es el orden el B-Tree. Esto es muy importante porque tenemos un gran ahorro en el número de accesos que tenemos que hacer ya que recordemos que estamos hablando de almacenamiento secundario.
Inserción
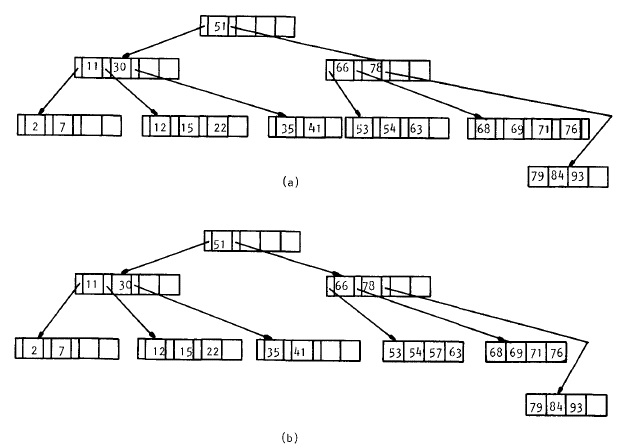
Analicemos como ocurren las inserciones en un árbol B-Tree. En la Figura 7.9 se presenta un B-Tree de orden 2, cada nodo en el árbol tendrá por consiguiente entre 2 y 4 llaves (debe existir un contador por cada nodo para saber rápidamente el número actual de llaves). La inserción es un proceso de 2 pasos, primero se debe realizar una búsqueda desde la raíz para localizar la "hoja" apropiada para insertar; a continuación la inserción se realiza y el balanceo se realiza por un procedimiento que mueve desde la hoja hasta la raíz.
Pongamos un ejemplo para ver este proceso más claramente. Deseamos insertar la llave "57" al B-Tree, lo primero que hacemos es buscar la posición que ocuparía, de manera que notamos que su lugar sería en el nodo donde estan (53,54,63), de manera que la llave se agrega y no se hace ningún otro movimiento adicional (Figura 7.9b)
|
Figura 7.9
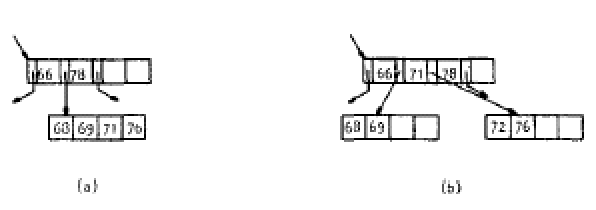
Por otro lado si quisiéramos insertar la llave "72" veríamos que su lugar sería en el nodo donde están (68,69,71,76) el cual como se puede observar ya se encuentra "lleno" de manera que debemos dividirlo (split) como se observa en la Figura 7.10. De manera que las llaves más pequeñas pertenecerán a uno de los nodos (68,69), las llaves más grandes al otro nodo (72,76) y finalmente la llave intermedia (71) se promocionará como separador en el nivel superior (acompañando al 66 y 78). Algo muy importante a considerar es qué sucede cuando esta "promoción" se hace hacia un nodo superior que ya se encuentra lleno, entonces ese nodo se deberá dividir y en caso de ser necesario se hará sucesivamente hasta llegar a la raíz en cuyo caso estaremos hablando de que el árbol habrá crecido en un nivel.
|
Figura 7.10
Eliminación
Esta operación de manera similar a la inserción requiere localizar la llave a borrar; posteriormente existen 2 posibilidades:
a) La llave se encuentra en un nodo "hoja"
b) La llave se encuentra en un nodo que no es una hoja.
Para el segundo caso se necesita que una llave adyacente sea encontrada para intercambiar posiciones y que la operación de búsqueda siga funcionando correctamente. Para ello simplemente se busca por la "leftmost leaf" o la hoja ubicada más a la izquierda del árbol derecho de la llave que deseamos eliminar.
|
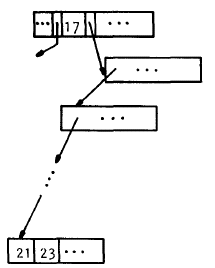
Figura 7.11
En la Figura 7.11 eliminamos la llave 17 y para ello debemos colocar en su lugar a la 21, pero algo importante que no se debe olvidar es que los nodos no pueden tener menos de "d" llaves, de manera que si en este caso el nodo que contenía a 21 queda con menos de "d" elementos entonces se produce un "underflow" y debemos hacer una redistribución de llaves.
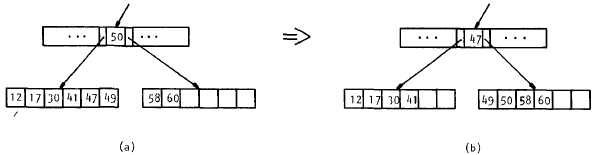
Para este último caso lo único que se necesita es una llave prestada desde una hoja vecina, pero como de todas formas se necesitan 2 lecturas a disco una mejor distribución se puede hacer, dividiendo las llaves que restan entre los dos nodos vecinos (Figura 7.12) de modo que se reducen los accesos de las próximas eliminaciones en ese nodo.
|
Figura 7.12
Obviamente esta distribución de llaves entre los 2 nodos funciona si al menos existen 2d llaves (sumando ambos nodos) de otra manera lo que se debe hacer es una "concatenación".
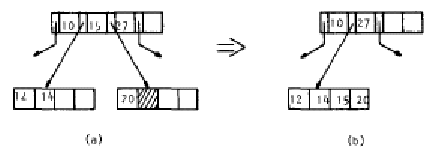
La concatenación consiste simplemente en unir las llaves de ambos nodos en uno solo y se "baja" la llave que servía de separador de manera que sea parte de este nuevo nodo (Figura 7.13)
Nota: en este caso el nodo que pierde el separador puede caer también en un underflow y el proceso se repetiría sucesivamente posiblemente hasta llegar a la raíz en cuyo caso el árbol se reducirá en un nivel.
|
Figura 7.13
Resumiendo:
- El B-Tree es el estándar para la organización de archivos
- Permite tener páginas (nodos) en las ramas del árbol
- Permite mantener ordenado el índice fácilmente
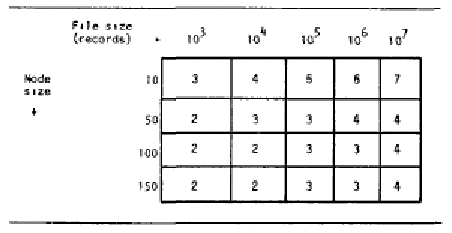
- Dependiendo del orden del b-tree, se puede obtener un gran rendimiento, por ejemplo si tenemos un b-tree de orden 25, el nodo tendrá 50 llaves y puede encontrar cualquier llave de entre 1,000,000 con tan solo 4 accesos a disco como se puede observar en las estadísticas de la Figura 7.14.
|
Knuth analizando el algoritmo de B-Trees propone una modificación al algoritmo bastante interesante:
-
Cada nodo se encuentra 2/3 lleno (en lugar del 1/2 del b-tree)
-
El "splitting" o la división de un nodo se "retarda" hasta que dos nodos hermanos se encuentren llenos
-
El Split entonces hará que 2 nodos se dividan en 3, cada uno 2/3 lleno
-
Garantiza al menos el 66% de utilización de espacio de almacenamiento
-
Sólo requiere algunas modificaciones al algoritmo
-
La altura del árbol es menor, en consecuencia las búsquedas son más rápidas.
-
El manejo de páginas es mayor