3. Modelo relacional
3.1 Introducción
En el capítulo anterior se mencionaron 3 tipos de modelado: conceptual, lógico y físico.
El modelo e-r se considera un modelo conceptual ya que permite a un nivel alto el ver con claridad la información utilizada en algun problema o negocio.
En este capítulo nos concentraremos en desarrollar un buen modelo "lógico" que se conoce como "esquema de la base de datos" (database schema) a partir del cual se podrá realizar el modelado físico en el DBMS, es importante mencionar que es un paso necesario, no se puede partir de un modelo conceptual para realizar un físico.
 |
3.2 Por qué "modelo relacional" ?
Puede resultar confuso el concepto de modelo entidad-relación vs modelo relacional, quizás porque ambos comparten casi las mismas palabras. Como se mencionó en la sección anterior, el objetivo del modelo relacional es crear un "esquema" (schema), lo cual como se mencionará posteriormente consiste de un conjunto de "tablas" que representan "relaciones", relaciones entre los datos.
Estas tablas, pueden ser construídas de diversas maneras:
- Creando un conjunto de tablas iniciales y aplicar operaciones de normalización hasta conseguir el esquema más óptimo. Las técnicas de nomalización se explican más adelante en este capítulo.
- Convertir el diagrama e-r a tablas y posteriormente aplicar también operaciones de normalización hasta conseguir el esquema óptimo.
La primer técnica fue de las primeras en existir y, como es de suponerse, la segunda al ser más reciente es mucho más conveniente en varios aspectos:
- El partir de un diagrama visual es muy útil para apreciar los detalles, de ahí que se llame modelo conceptual.
- El crear las tablas iniciales es mucho más simple a través de las reglas de conversión.
- Se podría pensar que es lo mismo porque finalmente hay que "normalizar" las tablas de todas formas, pero la ventaja de partir del modelo e-r es que la "normalización" es mínima por lo general.
- Lo anterior tiene otra ventaja, aún cuando se normalice de manera deficiente, se garantiza un esquema aceptable, en la primer técnica no es así.
3.3 Conceptos básicos
3.3.1 Tablas
El modelo relacional proporciona un manera simple de representar los datos: una tabla bidimensional llamada relación.
título |
año |
duración |
tipo |
| Star Wars | 1977 | 124 | color |
| Mighty Ducks | 1991 | 104 | color |
| Wayne's World | 1992 | 95 | color |
Relación Películas
La relación Películas tiene la intención de manejar la información de las instancias en la entidad Películas, cada renglón corresponde a una entidad película y cada columna corresponde a uno de los atributos de la entidad. Sin embargo las relaciones pueden representar más que entidades, como se explicará más adelante.
3.3.2 Atributos
Los atributos son las columnas de un relación y describen características particulares de ella.
3.3.3 Esquemas
Es el nombre que se le da a una relación y el conjunto de atributos en ella.
Películas (título, año, duración, tipo)
En un modelo relación, un diseño consiste de uno o más esquemas, a este conjunto se le conoce como "esquema relacional de base de datos" (relational database schema) o simplemente "esquema de base de datos" (database schema)
3.3.4 Tuplas
Cada uno de los renglones en una relación conteniendo valores para cada uno de los atributos.
(Star Wars, 1977, 124, color)
3.3.5 Dominios
Se debe considerar que cada atributo (columna) debe ser atómico, es decir, que no sea divisible, no se puede pensar en un atributo como un "registro" o "estructura" de datos.
3.3.6 Representaciones equivalentes de una relación
Las relaciones son un conjunto de tuplas, no una lista de tuplas. El orden en que aparecen las tuplas es irrelevante.
Así mismo el orden de los atributos tampoco es relevante
año |
título |
tipo |
duración |
| 1991 | Mighty Ducks | color | 104 |
| 1992 | Wayne's World | color | 95 |
| 1977 | Star Wars | color | 124 |
Otra representación de la relación Películas
3.4 Conversión del modelo e-r a un esquema de base de datos (Conversión a tablas)
3.4.1 Introducción
El modelo es una representación visual que gráficamente nos da una perspectiva de como se encuentran los datos involucrados en un proyecto u organización.
Pero el modelo no nos presenta propiamente una instancia de los datos, un ejemplo que muestre con claridad algunas datos de muestra y como se relacionan en realidad. Por eso es conveniente crear un "esquema", el cual consiste de tablas las cuales en sus renglones (tuplas) contienen instancias de los datos.
3.4.2 Conversión a tablas desde un modelo con relaciones (1-1,1-m,m-m)
Las tablas siguientes muestran las reglas que se deben seguir para poder crear dicho esquema.
modelo e-r conversión a tablas
|
 |
||||||||||||||||||||||||||||||
El diagrama anterior se convertiría al siguiente esquema: Debil
A
B1
B2
B3
A_B1
donde: LLP_X es la llave primaria de la entidad X (un subconjunto de atribs_X) |
Ejemplo:
 |
Para el ejemplo de la figura tendríamos el esquema:
escuela
departamento
curso
profesor
estudiante
profesor_curso
estudiante_curso
|
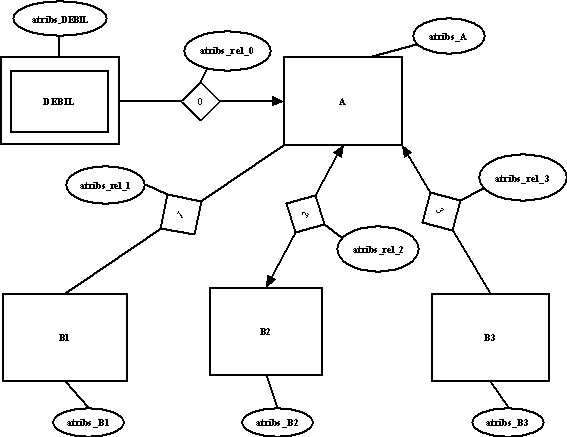
3.4.3 Conversión a tablas desde un modelo con generalización
modelo e-r
|
 |
||||||||||||||||||||
La generalización se convertiría al siguiente esquema: 1) A
B1
B2
B3
donde: LLP_X es la llave primaria de la entidad X (un subconjunto de atribs_X) |
||||||||||||||||||||
2) B1
B2
B3
donde: LLP_X es la llave primaria de la entidad X (un subconjunto de atribs_X) |
Es importante mencionar que a pesar de que existen 2 métodos para convertir una generalización a tablas, no hay una regla exacta de cual usar en determinado caso. A continuación se mencionan algunos consejos útiles para la determinación de cual método emplear:
- Si la entidad de nivel superior está relacionada con otra(s) entidades puede sugerirse emplear el método (1) ya que de esa manera la tabla (A) será la única involucrada en la relación, de otra forma se tendrían tres tablas (B1,B2 y B3) formando parte de la relación
- Es importante tomar en cuenta la pertenencia de instancias, si se considera que hablamos de una generalización disjunta, donde no se puede pertenecer a varias entidades de nivel inferior, quizás sea recomendable el método (1), en otro caso se podría pensar en el método (2).
- También es importante analizar ambos casos con respecto a las "consultas" que se deseen realizar ya que esto también determina en muchos casos el método a emplear.
3.4.4 Descubrimiento de llaves en las relaciones
Las llaves resultantes en las relaciones de un esquema se pueden inferir de la siguiente manera:
1) Cada tabla que provenga de una entidad contiene por si misma una llave
2) Para las tablas resultado de una relación se toman las llaves primarias de ambas entidades y éstas conforman la nueva llave primaria, excepto en un caso como el que sigue:
 |
|||||||||||||||
Podemos observar que existe una relación m-m entre "actor" y "serie", demostrando que un actor puede actuar en muchas series y que muchas series tendrán a los mismos actores. La tabla que se crearía sería: actor_serie
si se considera "id_actor, id_serie" como la llave primaria caemos en un problema porque esa combinación no identifica de manera única a la tupla, como es el caso de "Joaquín Pardavé, Génesis" ya que en la primer tupla tenemos que determina a "Abel hermano bueno" y en la tercera a "Caín hermano malo". La relación es correcta ya que un actor puede representar a varios personajes en la misma obra, pero entonces la llave "id_actor, id_serie" no es la correcta y en este caso lo más recomendable sería emplear los tres atributos de la relación "id_actor, id_serie, id_personaje" |
3.5 Normalización
Una vez creadas las tablas hay que verificarlas y revisar si aún se puede reducir u optimizar de alguna manera.
Los problemas tales como la redundancia que ocurren cuando se abarrotan demasiados datos en un sola relación son llamados anomalías. Los principales tipos son:
- Redundancia: la información se repite innecesariamente en muchas tuplas. En la relación siguiente, length y filmType.
- Anomalías de actualización: cuando al cambiar la información en una tupla se descuida el actualizarla en otra. Si en la relación encontramos que el length de StarWars es 125 podríamos cambiarlo únicamente para la primer tupla y olvidar actualizar las demás.
- Anomalías de eliminación: si un conjunto de valores llegan a estar vacíos y se llega a perder información relacionada como un efecto de la eliminación. Si eliminamos al actor Emilio Estevez, perdemos también la tupla de la película MightyDucks.
title |
year |
length |
filmType |
studioName |
starName |
Star Wars |
1977 |
124 |
color |
Fox |
Carrie Fisher |
Star Wars |
1977 |
124 |
color |
Fox |
Mark Hamill |
Star Wars |
1977 |
124 |
color |
Fox |
Harrison Ford |
Mighty Ducks |
1991 |
104 |
color |
Disney |
Emilio Estevez |
Wayne's World |
1992 |
95 |
color |
Paramount |
Dana Carvey |
Wayne's World |
1992 |
95 |
color |
Paramount |
Mike Meyers |
3.5.1 Dependencias funcionales (FD)
3.5.1.1 Definición
En el diseño de esquemas de bases de datos el concepto de dependencia funcional (functional dependency) es vital para eliminar "redundancia", otros factores sería el manejo de dependencias multivaluadas y las restricciones de integridad referencial.
Una dependencia funcional en una relación R es una enunciado de la forma "si dos tuplas de R concuerdan en los atributos A1,A2,...An (tienen los mismos valores para cada atributo), entonces deben concordar también con otro atributo B" . Esta FD se escribiría como A1,A2,....An --> B y se dice que "A1, A2,....An determina funcionalmente a B".
Por otro lado, si un conjunto de atributos A1,A2...An determina funcionalmente a más de un atributo,
A1, A2, ... An ---> B1
A1, A2, ... An ---> B2
A1, A2, ... An ---> Bm
entonces podemos simplemente escribir este conjunto de FDs como: A1, A2, ...An ---> B1,B2,...Bm
Movies(title, year, length, filmType, studioName, starName)
| title | year | length | filmType | studioName | starName |
| Star Wars | 1977 | 124 | color | Fox | Carrie Fisher |
| Star Wars | 1977 | 124 | color | Fox | Mark Hamill |
| Star Wars | 1977 | 124 | color | Fox | Harrison Ford |
| Mighty Ducks | 1991 | 104 | color | Disney | Emilio Estevez |
| Wayne's World | 1992 | 95 | color | Paramount | Dana Carvey |
| Wayne's World | 1992 | 95 | color | Paramount | Mike Meyers |
| ... |
title, year --> length
title, year --> filmType
title, year --> studioName
title, year -/-> starName
podemos entonces afirmar que: title, year --> length, filmType, studioName
Quizás las dependencias funcionales más evidentes sean las llaves.
Decimos que un conjunto { A1, A2,....An } es una llave de un relación si:
- Esos atributos determinan funcionalmente a "todos" los demás atributos de una relación.
- No hay un subconjunto de { A1, A2,....An } que determine funcionalmente a "todos" los demás atributos (incluyendo al resto del conjunto { A1, A2,....An })
La definición anterior de llave es similar a la que se mencionó anteriormente de superllave, sin embargo las superllaves no son llaves "mínimas", recordemos que una llave primaria se escoge de entre el conjunto de superllaves mínimas. Es importante hacer notar que una llave mínima no se refiere al número de atributos incluídos, se puede tener una llave mínima ABC y otra DE donde ambas son mínimas aún cuando una de ellas sea todavía de menor tamaño que la otra.
Al conjunto de dependencia funcionales de una relación R se le denominará F.
3.5.1.2 Axiomas de Armstrong:
- Reflexividad: sea
 un conjunto de atributos y
un conjunto de atributos y 

 entonces
entonces  -->
-->  *
* - Aumentación: si
 -->
--> y
y  es un conjunto de atributos entonces
es un conjunto de atributos entonces 
 -->
--> 

- Transitividad: si
 -->
-->  y
y  -->
--> entonces
entonces  -->
--> 
*Nota:
- De manera general una dependencia funcional de la forma
 -->
-->  se considera "dependencia funcional trivial" si
se considera "dependencia funcional trivial" si 


- Si al menos algún elemento de
 no pertenece a
no pertenece a  se considera una dependencia no trivial.
se considera una dependencia no trivial. - Si ningún elemento de
 pertenece a
pertenece a  entonces se considera una dependencia completamente no trivial
entonces se considera una dependencia completamente no trivial
3.5.1.3 Reglas adicionales
- Unión: si
 -->
-->  y
y  -->
-->  entonces
entonces  -->
--> 

- Decomposición: si
 -->
--> 
 entonces
entonces  -->
-->  y
y  -->
--> 
- Pseudotransitividad: si
 -->
-->  y
y 
 -->
-->  entonces
entonces 
 -->
--> 
3.5.1.4 Cerradura de un conjunto de atributos
Para un esquema R y un conjunto de atributos ![]() , si
, si ![]() --> R entonces
--> R entonces ![]() es superllave
es superllave
para determinar lo anterior se puede encontrar ![]() +, todos los atributos que dependen funcionalmente de
+, todos los atributos que dependen funcionalmente de ![]()
teniendo R(A,B,C,D,E)
si A+=(A,B,C,D,E), entonces A--> R entonces A es superllave
La cerradura se puede calcular siguiendo el siguiente algoritmo:
entrada: ![]() , F
, F
salida: ![]() +
+
result= while changes to result do for each ( begin if result=result end end |
result -->
|
teniendo R (A,B,C,D,E,F) y F las dependencias: AB-->C, BC-->AD, D-->E, CF-->B.
Comprobar que {A,B}+ ={A,B,C,D,E}
Si {A,B}+ = {A,B,C,D,E,F} entonces podríamos afirmar que AB es superllave, pero para ello sería necesaria alguna dependencia adicional ej. AB --> CF
El calcular la cerradura es empleado para:
- Verificar si
 es una superllave, calculando
es una superllave, calculando  + y revisando si
+ y revisando si  + contiene a todos los atributos de la relación R.
+ contiene a todos los atributos de la relación R. - Verificar una dependencia funcional
 -->
-->  (es decir, si pertenece a F+) checando si
(es decir, si pertenece a F+) checando si 

 +.
+. - Calcular F+ (la cerradura de todo el conjunto de dependencias F en una relación R): Para cada

 R se calcula
R se calcula  + y para cada elemento S
+ y para cada elemento S 
 + se obtiene una dependencia funcional
+ se obtiene una dependencia funcional  --> S.
--> S.
3.5.2 Primera forma normal
Una tabla se encuentra en 1a NF, si todos sus atributos son atómicos (indivisibles)
El ejemplo clásico:
| nombre | dirección | teléfono |
En 1a. NF
| nombre | apellido_paterno | apellido_materno | dirección | teléfono |
3.5.3 Segunda forma normal
Una tabla se encuentra en 2a NF, si está en 1a NF y cada atributo que NO es llave es "completamente" dependiente de la llave.
Si tenemos la tabla:
calificaciones_cursos
| id_estudiante | depto | clave_curso | descripción | calificación |
NO se encuentra en 2a NF ya que
{ id,clave,depto} --> descripción
{clave,depto} --> descripción
Analizando todas las dependencias funcionales:
{ id,clave,depto} --> descripción
{clave,depto} --> descripción
{ id,clave,depto} --> calificación
Para realizar la normalización (2NF) la relación se descompondría en:
|
La descomposición se basa básicamente en:
- La intuición
- Las dependencias funcionales
Es importante que al descomponer una relación exista:
- Descomposición sin pérdida
- Preservación de dependencias funcionales
3.5.4 Descomposición sin pérdida
Al descomponer una relación R en varias relaciones R1 y R2 se debe verificar que no haya pérdidas, es decir, que al volver a combinar las relaciones (producto entre R1 y R2) se obtengan exactamente las mismas tuplas.
Decimos entonces que para una descomposición en R1 y R2 no hay pérdida si:
{ R1 ![]() R2 --> R1 }
R2 --> R1 } ![]() F+
F+
o bien si
{ R1 ![]() R2 --> R2 }
R2 --> R2 } ![]() F+
F+
Para el ejemplo anterior la relación
id_estudiante depto clave_curso descripción calificación F={ { id,clave,depto} --> descripción, {clave,depto} --> descripción, { id,clave,depto} --> calificación }
tiene F+= { { id,clave,depto} --> id,clave,depto,descripción,calificación, {clave,depto} --> descripción }
y dicha relación se descompone en:
depto clave_curso descripción
id_estudiante depto clave_curso calificación
donde R1
R2 = depto,clave_curso donde depto,clave_curso -->descripción
y {depto,clave_curso -->descripción}
{ { id,clave,depto} --> id,clave,depto,descripción,calificación, {clave,depto} --> descripción }
3.5.5 Preservación de dependencias
Al descomponer una relación R en varias relaciones R1,R2,..Rn es importante revisar que se preserven las dependencias funcionales iniciales. De esta manera se garantiza que una actualización no provoque una relación inválida, verificando las FDs o bien a través de combinaciones de relaciones(productos o joins) aunque esto último no es muy eficiente.
Para ello se analizan todas la dependencias funcionales Fi para cada Ri que deberán ser un subconjunto de F+
De manera que F' = F1 ![]() F2
F2 ![]() ...Fn
...Fn
y la preservación se verifica si F'+= F+
para el ejemplo anterior teniendo:
F={ { id,clave,depto} --> descripción, {clave,depto} --> descripción, { id,clave,depto} --> calificación }
F+= { { id,clave,depto} --> id,clave,depto,descripción,calificación, {clave,depto} --> descripción }
F1= depto,clave_curso--> descripción
F2= id_estudiante,depto,clave_curso --> calificación
F' = F1
F2
depto,clave_curso--> descripción
id_estudiante,depto,clave_curso --> calificación
F'+= { { id,clave,depto} --> id,clave,depto,descripción,calificación, {clave,depto} --> descripción }
y como F'+= F+ entonces si hay preservación de dependencias.
3.5.6 Forma normal de Boyce-Codd (BCNF)
3.5.6.1 Características
Un esquema relacional se encuentra en BCNF si para toda dependencia funcional X --> A:
- X --> A es una dependencia funcional trivial
o
- X es una super llave
BCNF no necesariamente preserva las dependencias funcionales F'+ != F+
3.5.6.2 Algoritmo general de descomposición tratando de alcanzar BCNF
result= {R}
done=false calcular F+ while (! done) do if(existe un esquema Ri en result que no está en BCNF) then si result= ( result - Ri )
else done=true end |
Ejemplo:
R(A,B,C,D)
B--> C |
(B)+ = {CD} |
| B-->D |
La superllave sería {AB} por lo tanto no cumple con BCNF
(B-->CD y B no es superllave).Descomponiendo usando B-->CD
(A,B) (B,C,D)
Esta última en BCNF
3.5.7 Tercera forma normal
3.5.7.1 Características
Un esquema relacional se encuentra en 3NF si para toda dependencia funcional X --> A:
- X --> A es una dependencia funcional trivial
o
- X es una super llave
o
- A es miembro de una llave candidata de R
Lo anterior no quiere decir que una sola llave candidata deba contener a todos los atributos de A, cada atributo de A puede estar contenido en llaves candidatas diferentes.
Se puede observar que las 2 primeras restricciones son las mismas que para BCNF pero existe una tercera que da flexibilidad a las relaciones.
Podemos afirmar entonces que: "Si una relación está en BCNF, está también 3NF; pero si una relación está en 3NF no necesariamente está en BCNF".
ejemplo, dada la relación
branch-name |
customer-name |
banker-name |
office-number |
banker-name --> branch-name office-number
customer-name branch-name --> banker-name
Se puede observar {customer-name branch-name} determina al resto de los atributos así que es la superllave de R.
No está en 3NF porque:
- Las DFs no son triviales
- En la primer dependencia, "banker-name" no es superllave de R
- Se puede observar que office-number y banker-name no son parte de alguna llave candidata
se descompondría en:
banker-name |
branch-name |
office-number |
banker-name --> branch-name office-number
customer-name |
branch-name |
banker-name |
customer-name branch-name --> banker-name
banker-name --> branch-name
Esta descomposición si está en 3NF porque:
- No hay dependencias funcionales triviales
- En la segunda relación, la segunda DF no cumple que banker-name es superllave
- En la segunda relación, la segunda DF, branch-name es miembro de la llave candidata
{customer-name, branch-name}
Al cumplirse la 3er regla se confirma que la descomposición está en 3NF.
Se puede observar que al no cumplir con las 2 primeras no está en BCNF pero gracias al relajamiento si está en 3NF
Otro ejemplo:
deptos
nombre_depto extensión id_jefe nombre_depto --> extensión, jefe
empleados
id_empleado nombre_depto id_jefe id_empleado --> nombre_depto, id_jefe
nombre_depto --> id_jefe
No está en 3NF porque:
- Las DFs no son triviales
- En la dependencia "nombre_depto-->id_jefe" de la segunda relación, "nombre_depto" no es superllave de R
- Se puede observar nuevamente para la segunda relación que id_jefe no es parte de alguna llave candidata
Aplicando la descomposición:
nombre_depto --> extensión, jefe
id_empleado --> nombre_depto |
Esta descomposición si está en 3NF porque:
- No hay dependencias funcionales triviales
- Para toda dependencia X--> A , X es superllave.
Se observa como la relación no solo está en 3NF sino también en BCNF por cumplir con la segunda regla.
3.5.7.2 Algoritmo general de descomposición tratando de alcanzar 3NF
3.5.7.2.1 Forma canónica de las FDs (Fc)
La forma canónica de F es aquel conjunto mínimo de dependencias funcionales equivalentes a F, sin dependencias redundantes o partes redundantes de dependencias.
Para obtener la Fc se deben extraer todos los miembros "extraños", suponga un conjunto F de dependencias funcionales y la dependencia ![]() -->
--> ![]() está en F.
está en F.
- El atributo A es extraño en
 si A
si A 
 y
y
F lógicamente implica (F - { -->
-->  })
})  { (
{ ( - A ) -->
- A ) -->  }
}
Ejemplo:
F = { A --> C , AB --> C }B es extraño en AB --> C porque { A --> C, AB --> C } lógicamente implica A --> C (el resultado de quitar B de AB --> C ).
- El atributo A es extraño en
 si A
si A 
 y
y
el conjunto de dependencias (F - { -->
-->  })
})  {
{  --> (
--> ( - A ) } implica lógicamente a F
- A ) } implica lógicamente a F
Ejemplo:
F = { A --> C , AB --> CD}C es extraño en AB --> CD porque A B --> C puede ser inferido aún después de eliminar C
Test para verificar si un atributo es extraño
Dado un conjunto de dependencias F y ![]() -->
--> ![]() está en F
está en F
- Para verificar si A

 es extraño en
es extraño en 
- calcular ( {
 } - A )+ usando las dependencias en F
} - A )+ usando las dependencias en F - verificar si ( {
 } - A )+ contiene a
} - A )+ contiene a  , si lo hace entonces A es extraño
, si lo hace entonces A es extraño
- calcular ( {
- Para verificar si A

 es extraño en
es extraño en 
- calcular
 + usando solo las dependencias en:
+ usando solo las dependencias en:
F'=(F - {
 -->
-->  })
})  {
{  --> (
--> (  - A) }
- A) } - verificar si
 + contiene a A, si lo hace entonces A es extraño
+ contiene a A, si lo hace entonces A es extraño
- calcular
3.5.7.2.2 Algoritmo basado en Fc
Fc: Forma canónica de las FDs
|
*El algoritmo anterior garantiza que en una descomposición no haya pérdida (al incluir por lo menos en una relación una de las superllaves) y que se preserven las dependencias funcionales (al incluir cada una de ellas).
Ejemplo:
sid |
name |
street |
city |
zip |
student
Fc:
sid -->name,street,city
street, city-->zip
zip --> cityDescomponer en 3NF
- R1(sid, name, street, city), R2(zip, street, city), R3(zip, city)
- -
- -
- Eliminar R3
R1
sid -->name,street,city
R2street, city-->zip
zip --> city
3.5.8 BCNF vs 3NF
Como se mencionó anteriormente: "Si una relación está en BCNF, está también 3NF; pero si una relación está en 3NF no necesariamente está en BCNF".
En la práctica la mayoría de los esquemas en 3NF también están en BCNF, contraejemplo:
(Sucursal, Cliente, Banquero)
banquero --> sucursal
sucursal, cliente --> banquero
está en 3NF pero no en BCNF puesto que "banquero" no es una superllave, normalizando:
suc-banquero (sucursal, banquero)
suc-cliente (sucursal, cliente)
Nuevamente se presentan las pérdidas de dependencias
Qué es mejor ? BCNF o 3NF ?
- De manera general se puede decir que ambas son buenas.
- El caso ideal es conseguir BCNF sin pérdidas y con preservación de dependencias.
- Si se alcanza BCNF pero no hay preservación de dependencias se puede considerar una 3NF (recordando que 3NF siempre debe carecer de pérdidas y debe preservar dependencias).
3.6 Conclusiones
De manera que las metas del diseño de bases de datos con dependencias funcionales son:
- BCNF*
- Descomposición sin pérdida
- Preservación de dependencias
* Llegar a una forma BCNF puede llegar a ser complicado, debido a esto en muchas ocasiones es suficiente con alcanzar la 3NF para lograr un buen diseño.